Models of Population Genetics
It is often said that there are four main processes which drive the evolution of a population: genetic drift, mutation, selection, and migration. Genetic drift is the process by which the genetic composition of a population changes due solely to random reproduction events. Accounting for the influence of genetic drift therefore requires a stochastic approach.
Typically, models are formulated in terms of a fixed population of N individuals, of different types. The most simple example is the haploid Moran model. Individuals have a single allele, A or B. We can then denote the number of A's as n and the number of B's as m = N - n. In the absence of selection (i.e. when neither A nor B has a fitness advantage) the system is said to be neutral and the dynamics take on a particularly simple form ...
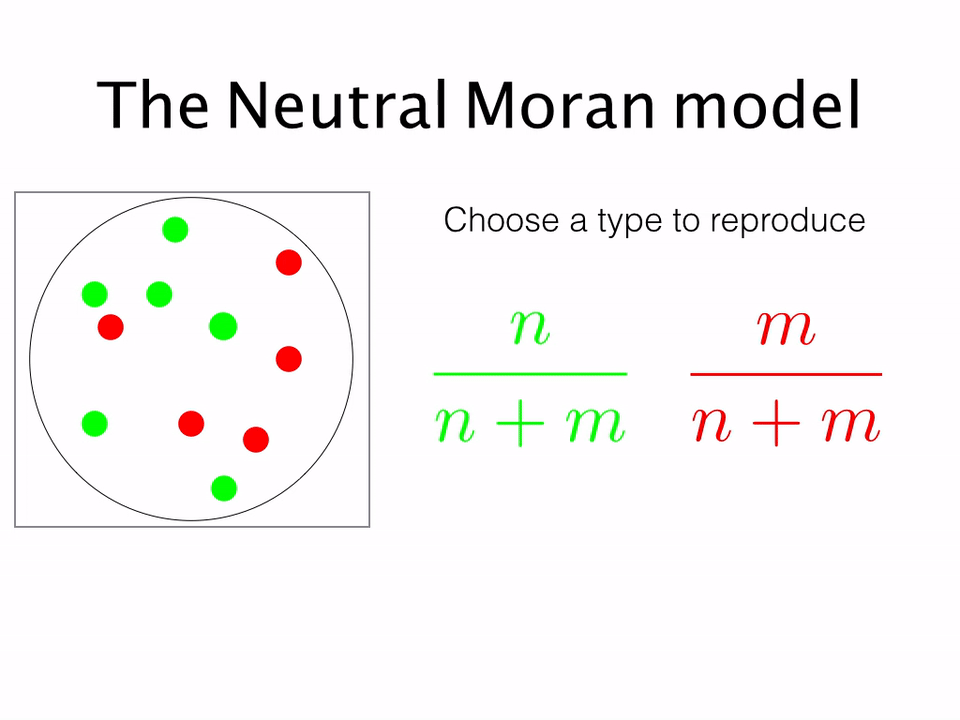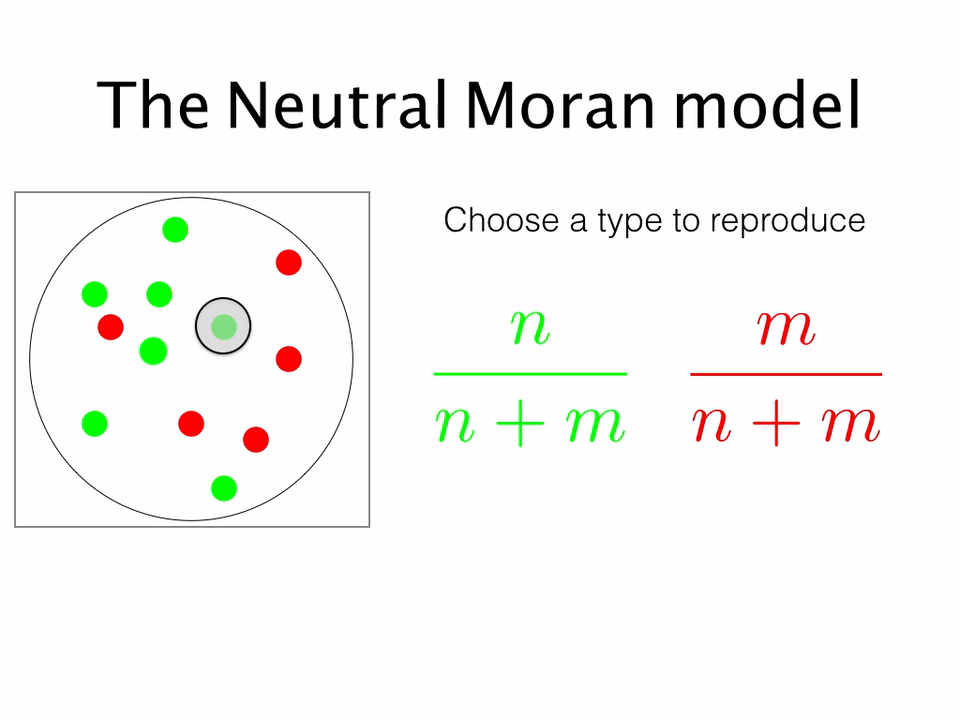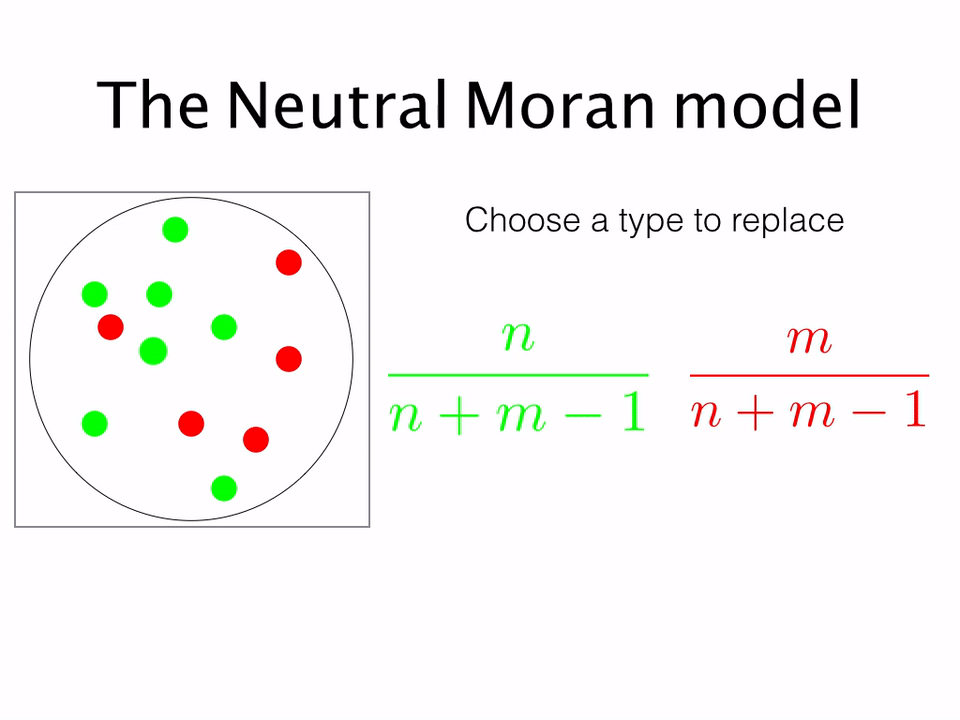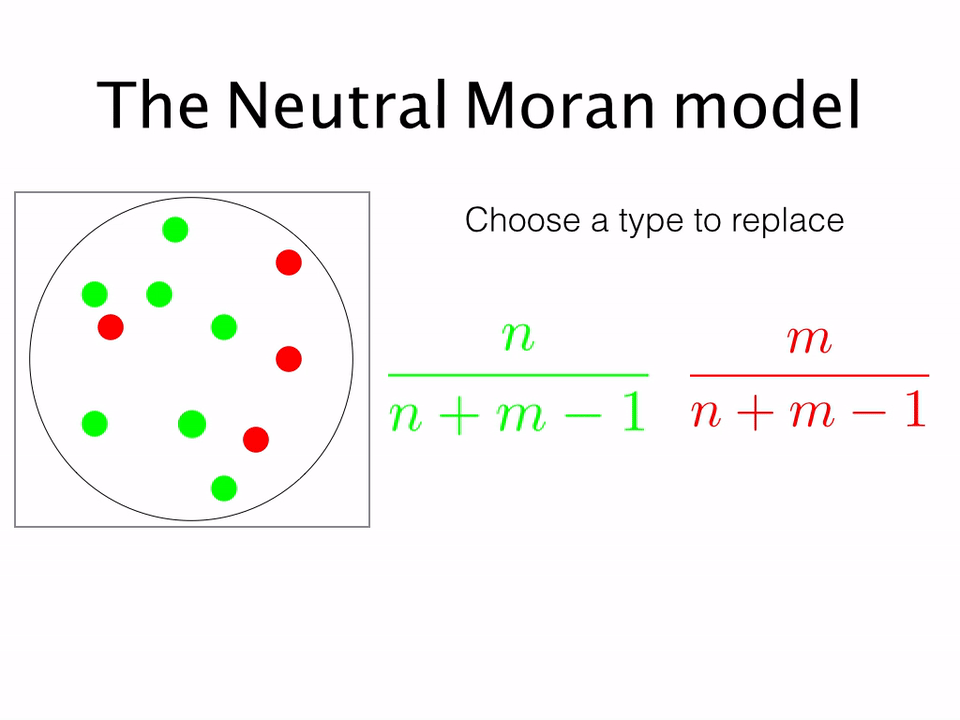
Replicating this process over and over again, one obtains the stochastic dynamics for the system. While for a population of infinite size (the deterministic limit) the population composition does not change with time, for any real finite population it is clear that eventually either A or B will come to randomly fixate in the population. Analytically calculating the probability of either type fixating in the presence of both space and selection was the focus of my following papers ...
Population genetics on islands connected by an arbitrary network: an analytic approach
Fast-mode elimination in stochastic meta-population models
while I calculated the additional effect of mutation processes in
Stationary solutions for metapopulation Moran models with mutation and selection.
