Fast-Variable Elimination
It is possibly only a slight exaggeration to say that of all the mathematical models we can dream of, there are only two kinds which are straightforward to solve: those which are linear, and those which are one-dimensional. This aphorism holds equally for stochastic dynamical systems as it does for their deterministic counterparts.
However, if a separation of timescales exists, it is sometimes possible to extricate the dynamics happening on a fast timescale from those occurring on a slow timescale. We can thus achieve a reduction in the dimensionality of the system, which may make an analysis possible or simply improve our intuition as to how the system behaves. Developing and utilizing methods for the removal of fast-variables from stochastic population models formed the focus of my PhD research.
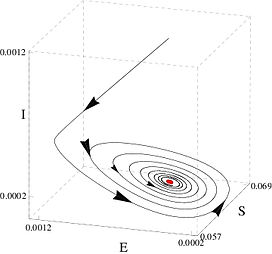
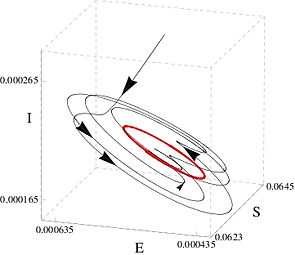
As an example, consider the panels below. The deterministic dynamics are given for an SEIR epidemiological model without and with seasonal forcing (left and right respectively). In this model, the disease dynamics (infection and recovery) occur on a much fast timescale than those of birth and death. Consequently, the system quickly relaxes to a subspace (the 2D plane) of lower dimension than the entire variable space (the SIR cube). We can approximate the dynamics as being restricted to this low-dimensional subspace, reducing the complexity of the problem.